グラフ理論,ゲーム理論
ヤマダ タイキ
山田 大貴
助教
| 学部等 |
総合理工学部
数理科学科
|
|---|---|
| researchmap 個人URL |
https://researchmap.jp/taikiyamada |
| SDGs |
|
| ホームページURL |
産業分野
- 教育,学習支援業 / 学校教育
- 情報通信業 / 通信業
- 情報通信業 / 情報サービス業
- 学術研究,専門・技術サービス業 / 学術・開発研究機関
researchmap
研究分野
- 自然科学一般 / 幾何学
- 自然科学一般 / 応用数学、統計数学
- 人文・社会 / 理論経済学
研究キーワード
グラフ理論,データ分析,幾何学
研究概要
点と線から構成される離散的図形のグラフは,18世紀頃から研究されており,グラフの構造や性質を明らかにする学問をグラフ理論と呼び,理論的に重要な研究対象である.一方,結晶格子や電子回路やネットワークといった対象と対象の結びつきが重要とされる現象に対して,グラフを用いて数理モデルを作成して分析することができるため,グラフは実践的にも重要とされている.
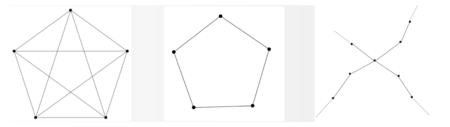
近年は,ビックデータの数理モデルにもグラフが用いられることから,点や線が複雑化しており,局所的な情報から大域的な性質が得られるような理論構築が求められている.そこで,リーマン幾何学において多様体の構造を調べる際に用いられる「リッチ曲率」をグラフに応用する研究が2010年ごろから開始された.グラフのリッチ曲率は各辺について計算され,リッチ曲率の値が大きくなればなるほど辺の"密集度"が増すことが確認できる.(研究概要の図を参照)このグラフのリッチ曲率を無向グラフだけでなく有向グラフや単体的複体,ハイパーグラフといった様々な離散対象へ拡張したのが私の研究になる.
近年は,ビックデータの数理モデルにもグラフが用いられることから,点や線が複雑化しており,局所的な情報から大域的な性質が得られるような理論構築が求められている.そこで,リーマン幾何学において多様体の構造を調べる際に用いられる「リッチ曲率」をグラフに応用する研究が2010年ごろから開始された.グラフのリッチ曲率は各辺について計算され,リッチ曲率の値が大きくなればなるほど辺の"密集度"が増すことが確認できる.(研究概要の図を参照)このグラフのリッチ曲率を無向グラフだけでなく有向グラフや単体的複体,ハイパーグラフといった様々な離散対象へ拡張したのが私の研究になる.
アピールポイント
数学を諸科学に応用させることに対して興味があります.
文理融合で研究していけたらと思います.